Word2Vec Paper Understanding

Word2Vec and Corresponding Knowledge

1. Neural Network language model

1.1 CBOW(Continue bag of words)

CBOW最早是Mikolov等大牛在2013年提出的。CBOW要利用若干个上下文词来预测中心词。之所以称为continuous bag-of-word，即连续词袋，是因为在考虑上下文单词时，这些上下文单词的顺序是忽略的。我们先从最简单版本的CBOW开始讲，即上下文词只有1个。

One-word context

先从最简单的CBOW开始讲，即只使用1个上下文单词$w_I$来预测中心词$w_O$。
如图1描述的就是One-word context定义之下的神经网络模型。词典大小为V, 隐藏层的大小为N，相邻层的神经元是全连接的。输入层是一个用one-hot方式编码的单词向量$x=(x_1,…x_k,…,x_V)$，其中只有一个$x_k$为1，其余均为0。

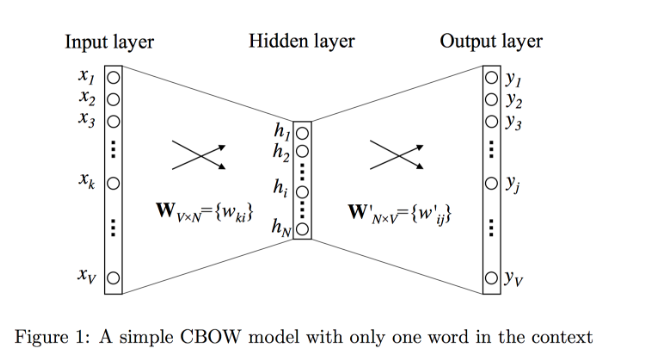
输入层到隐藏层
输入层到隐藏层的连接权重可以表示使用$W_{V \times N}$:

$$\mathbf W= \begin{pmatrix} w_{11}& w_{12}& …& w_{1N}\\ w_{21}& w_{22}& … & w_{2N}\\ …& … & … & …\\ w_{V1}& w_{V2}&. .. &w_{VN} \end{pmatrix}$$

$W_{V \times N}$每行是相应单词的输入词向量表示，即第一行为词典中第一个单词的输入词向量表示，第$k$行为词典中第$k$个词的输入词向量表示，解释如下：

$$\mathbf h= \mathbf W^T \mathbf x=\mathbf W_{(k,\cdot)}^T :=\mathbf v_{\omega_I}^T \tag{1}$$

$x$是某个单词的one-hot向量表示，且该单词在词典中的下标为k，即$x_k$=1, $x^\prime_k=0, k^\prime≠k$。因此只用到$W^T$的第$k$列，也即$W$的第$k$行。因此，$W$的第$k$行即为第k个单词的输入词向量，相当于直接将$W$的第$k$行拷贝到隐藏层单元$h$上。该输入词向量也是我们最终学习到的词向量（后面的输出词向量我们不需要）。

在上述神经网络中，相当于输入层到隐藏层的激活函数为线性激活函数。另外，由于具有上述的性质，因此通常输入层到隐藏层不显示绘制出来，直接通过查表操作(如TensorFlow中embedding_lookup)拿出单词的词向量，然后传入到下一层，只不过这个词向量也需要通过反向传播来优化。

隐藏层到输出层
从隐藏层到输出层，同样有连接权重矩阵$W′_{N×V}=w′_{ij}$来表示。注意，$W$和$W′$不是转置的关系，是不同的两个矩阵。$W′$用于预测输出词向量。

$$\mathbf W’= \begin{pmatrix} w_{11}^{\prime}& w_{12}^{\prime}&… & w_{1V}^{\prime}\\ w_{21}^{\prime} &w_{22}^{\prime}&…&w_{2V}^{\prime}\\ …&…&…&…\\ w_{N1}^{\prime} &w_{N2}^{\prime}&…&w_{NV}^{\prime} \end{pmatrix}$$

$W′$的每一列可以解释为相应单词的输出词向量，即：第一列为词典中第一个单词的输出词向量表示，第$k$列为词典中第k个词的输出词向量表示，记做$v′_{w_k}$。
计算输出层每个单元$j$的未激活值，这个$j$就是基本定义中的输出单词(标签)在词典中的下标。

$$u_j = {v^{\prime}_{w_j}}^T h \tag{2}$$

$v^\prime_{w_j}$是$W^\prime$的第$j$列，$h$实际上就是某个样本对$(w_I,w_O)$中的$w_I$的输入词向量（CBOW中为上下文词的输入词向量），当$O=j$时，$v^\prime_{w_j}$实际上就是$w_O$的输出词向量（CBOW中为中心词的输出词向量），因此$u_j$衡量了二者的相似性，也就是共现性。

计算输出层每个单元$j$激活值，使用softmax激活函数，这个激活值就是用来近似输出单词的后验概率分布，该分布是词典上所有单词的多项式分布：$Mult(V, \mathbf p(w_j|w_I)), j=1,2…,V$，即词典上所有输出单词$w_j$都有一个作为上下文单词的中心词的概率，所有概率和为1。

$$p(w_j|w_I) = y_j = softmax(u_j) = \frac{exp(u_j)}{\sum_{j^{\prime}=1}^V exp(u_{j^{\prime}})} \tag{3}$$

$y_j$是第$j$个输出神经元的激活值.

(1)、(2)代入(3)得到：

$$p(w_j|w_I)=\frac{\exp({\mathbf v_{w_j}’}^T \mathbf v_{w_I})}{\sum_{j’=1}^V\exp({\mathbf v_{w_j}’}^T \mathbf v_{w_I})} \tag{4}$$

我们的优化目标是，对于$j=O,p(w_j|w_I)→1$, 对于$j≠O$,$p(w_j|w_I)→0$
但是这个式子是优化难点，分母上需要计算每个输出单词的未激活值，计算复杂度太高。这也是后面优化技术出现的原因。
再强调一遍，对于某个单词$w$，$v_w$和$v^\prime_w$是单词的两种向量表示形式。其中$v_w$实际上是权重矩阵$W$（input->hidden）的某一行向量，$v^\prime_w$则是权重矩阵$W′$（hidden->output）的某一列向量。前者称作输入向量，后者称作输出向量。

损失函数定义和优化
1）损失函数定义
分母上需要计算每个输出词的未激活值，计算复杂度过高，实践中这种方法是行不通的，因此需要优化。下面给出CBOW模型的损失函数和梯度计算方法。

这里使用的损失函数实际上是交叉熵损失函数$E=−∑_jc_jlogp(x_j)$($x_j$理解为输入one_hot样本，$p$理解为整个神经网络, 因此$p(x_j)$在该问题中就是最终的输出神经元激活值$y_j$)。$c_j$是样本$x_j$的真实标签，对于某个样本实例，在输出神经元上，只有一个分量的$c_j=1$，其余为0，不妨令这个分量为$j^∗$。化简即：$E=−logp(w_O|w_I)$为本问题的交叉熵损失函数。推导：对于单样本而言，最大化似然概率：

$$\begin{align} & \max p(w_O|w_I)=\max y_{j^{*}} \tag{5}\\ &=\max \log y_{j^{*}} \tag{6}\\ &=u_{j^{*}} - \log \sum_{j^{\prime}=1}^V \exp(u_{j^{\prime}}):=-E \tag{7} \end{align}$$

即：

$$E = -u_{j^{*}} + log \sum_{j^{\prime}=1}^V exp(u_j^{\prime})$$

接下来使用梯度下降和误差反向传播进行优化，这部分比较简单，具体推导不细说，下面是对单个样本实例的更新公式。
2）输出层到隐藏层
先求$E$对$u_j$的导数：

$$\frac{\partial E}{\partial u_j}=y_j-t_j:=e_j \tag{8}$$

当$j=j^∗$时，$t_j=1$, 否则$t_j=0$。（损失的第一项）、损失第二项求导后就是激活值$y_j$。

再求$E$关于权重矩阵$W^\prime$的元素$w_{ij}′$的导数，一个元素$w^\prime_{ij}$只和隐藏层神经元$h_i$、输出层未激活神经元$u_j$相连接。

$$\frac{\partial E}{\partial w_{ij}’}=\frac{\partial E}{\partial u_j}\cdot \frac{\partial u_j}{\partial w_{ij}^{\prime}}=e_j\cdot h_i \tag{9}$$

使用SGD更新$w^\prime_{ij}$:

$$\begin{align} {w_{ij}^{\prime}}^{(new)}={w_{ij}^{\prime}}^{(old)}-\eta \cdot e_j \cdot h_i\tag{10} \end{align}$$

或者一次性更新输出神经元$j$对应的单词$w_j$的输出词向量$v_{w_j}^\prime$，也即$W′$的第$j$列（输出神经元$j$的误差$e_j$传播到和它相连的权重向量$v_{w_j}^\prime$）

$$\begin{align} {\mathbf v_{w_j}^{\prime}}^{(new)}= {\mathbf v_{w_j}^{\prime}}^{(old)} - \eta \cdot e_j \cdot \mathbf h \space \space \text{for} \ \ j=1,2,…V.\tag{11} \end{align}$$

由公式（11）可以看出，在更新权重参数的过程中，我们需要检查词汇表中的每一个单词，计算出它的激活输出概率$y_j$（源于多分类，soft-max分母），并与期望输出$t_j$（取值为0或者1）进行比较，$t_j$实际上就是真实标签，对于某个样本，若某个输出词为该样本的中心词，则为1，否则为0。也就是说，对于某个样本实例$(w_I,w_O)$，不仅要计算$p(w_O|w_I)$， 还要计算$p(w_j|w_I)， j=1,2…,V$。对于某个样本实例$(w_I,w_O)$，我们希望优化的结果是，对于真实中心词$w_O$，$p(w_O|w_I)$概率接近1，对于其他非真实中心词$wj$, $p(w_j|w_I)$概率接近0。

梯度更新解释性如下，
i）如果$y_j>t_j$ (“overestimating”)，则预测$w_j$作为中心词的概率值过大了，也就是说这个输出词$w_j$没有这么大可能作为上下文词$w_I$的中心词，或者说这个中心词和上下文词差别应当更大。那么优化的结果，就从向量$v′_{w_j}$中减去隐藏向量$h$的一部分（即上下文词$w_I$的输入词向量$v_{w_I}$），这样向量$v′_{w_j}$就会与向量$v_{w_I}$相差更远。
ii）如果$y_j<t_j$（“underestimating”)，这种情况只有在$t_j=1$时才会发生，此时$w_j=w_O$，也就是预测$w_j$作为中心词的概率值过小了，这个输出词$w_j$有很大可能就是上下文词$w_I$的中心词，或者说这个中心词和上下文词差别很小。那么优化的结果是，将隐藏向量h的一部分加入$v′_{w_O}$，使得$v′_{w_O}$与$v_{w_I}$更接近。
iii）如果$y_j$与$t_j$非常接近，则此时$e_j$非常接近于0，故更新参数基本上没什么变化。
上述远近是针对向量内积而言，也即在向量空间中两个点的距离。可以证明：

$$(v+\alpha h)^T \cdot h > v^T \cdot h \rightarrow \text{加上h的某比例分量，则和h更接近} \\ (v-\alpha h)^T \cdot h < v^T \cdot h \rightarrow \text{减去h的某比例分量，则和h更远离} \\ \alpha > 0$$

3) 隐藏层到输入层
先求$E$对隐藏层神经元$h_i$的偏导，$h_i$和所有输出神经元j都有连接，故求和计算收集到的所有误差。

$$\frac{\partial E}{\partial h_i} = \sum_{j}^V \frac{\partial E}{\partial u_j} \cdot \frac{\partial u_j}{\partial h_i} = \sum_j e_j w_{ij}^{\prime} :=EH_i \tag{12}$$

$EH$是$N$维向量，$EH=W′_{N×V}⋅e_{V×1}=∑^V_{j=1}e_j×v′_j$

再求$E$对$W$元素$w_{ki}$的导数， $h_i$和$w_{ki},k=1,2…,V$权重相连。

$$h_i=\sum_{k=1}^V x_k \cdot w_{ki} \tag{13}$$

有：

$$\frac{\partial E}{\partial w_{ki}}=\frac{\partial E}{\partial h_i} \cdot \frac{\partial h_i}{\partial w_{ki}}=EH_i \cdot x_k \tag{14}$$

对于某个样本而言，只有一个分量$x_k=1$,其余为0，因此一个样本实际上只更新$W$的第$k$行向量。
写成矩阵更新的形式：

$$\begin{align} \frac{\partial E}{\partial \mathbf W} &= \begin{pmatrix} \frac{\partial E}{\partial w_{11}}& \frac{\partial E}{\partial w_{12}}& …& \frac{\partial E}{\partial w_{1N}}\\ \frac{\partial E}{\partial w_{21}}& \frac{\partial E}{\partial w_{22}}& … & \frac{\partial E}{\partial w_{2N}}\\ …& … & … & …\\ \frac{\partial E}{\partial w_{V1}} & \frac{\partial E}{\partial w_{V2}} &. .. & \frac{\partial E}{\partial w_{VN}} \end{pmatrix} \\ &= \begin{pmatrix} EH_1 \cdot x_1 & EH_2 \cdot x_1 & …& EH_N \cdot x_1\\ EH_1 \cdot x_2 & EH_2 \cdot x_2 & …& EH_N \cdot x_2\\ …& … & … & …\\ EH_1 \cdot x_V & EH_2 \cdot x_V & …& EH_N \cdot x_V\\ \end{pmatrix} \\ &= \mathbf x \otimes \mathbf{EH} = \mathbf x \mathbf{EH}^T \end{align} \tag{15}$$

更新输入词向量$v_{w_I}$:

$${\mathbf v_{W_I}}^{(new)}={\mathbf v_{W_I}}^{(old)}-\eta \cdot \mathbf {EH}^T \tag{16}$$

也就是说，对于某个样本而言，上述$x_1,x_2,…,x_V$只有1个值非0。那么式15更新中，只有该行非零，其余行全为0。因此，我们只更新输入上下文词$w_I$对应行的词向量。
该梯度更新过程可以使用同样的解释方法，$EH=W′_{N×V}⋅e_{V×1}$，意味着：

i）如果过高地估计了某个单词$w_j$作为最终输出中心词的概率（即：$y_j>t_j$），相应$e$分量$e_j$大于0，则(16)式更新相当于将$v_{W_I}$输入上下文词向量第$j$个分量减去输出中心词$v_{w_j^\prime}$词向量的第$j$个分量，使得二者远离。

ii）如果过低地估计了某个单词$w_j$作为最终输出中心词的概率（即：$y_j<t_j$），相应$e$分量$e_j$小于0，则(16)式更新相当于将$v_{W_I}$输入上下文词向量第$j$个分量加上输出中心词$v′_{w_j}$词向量的第$j$个分量，使得二者接近。

因此，上下文单词$w_I$（context word ）的输入向量的更新取决于词汇表中所有单词预测为中心词的误差$e$。预测误差越大，则该单词对于上下文单词的输入向量的更新过程影响越大。

Multi-word context

基于multi-word context的CBOW模型利用多个上下文单词来预测中心单词，且不同上下文单词不考虑顺序。神经网络结构如图2所示：

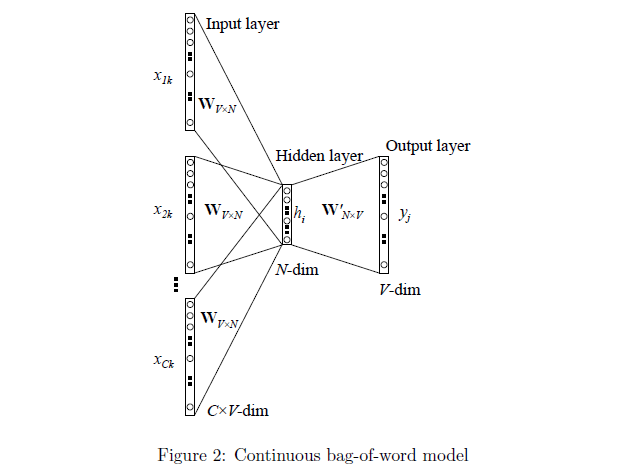
其隐藏层的输出值的计算过程为：首先将输入的上下文单词（context words）的向量相加起来并取其平均值，接着与input→hidden的权重矩阵相乘，作为最终的结果，公式如下：

$$\begin{align} & \mathbf h = \frac{1}{C} \mathbf W^T(\mathbf x_1 + \mathbf x_2 + \cdots +\mathbf x_C)\tag{17}\\ & = \frac{1}{C}(\mathbf v_{w_1}+\mathbf v_{w_2} + \cdots+\mathbf v_{w_C})^T\tag{18} \end{align}$$

C为上下文单词的数量，$w_1,w_2,…,w_C$为上下文单词，$v_w$是上下文单词$w$的输入词向量。
损失函数如下：

$$\begin{align} & E = - \log p(w_O|w_{I,1},…,\omega_{I,C}) \tag{19}\\ & =- u_{j^{*}} + \log \sum_{j^{\prime}=1}^{V} exp(u_{j^{\prime}})\tag{20}\\ & = - {\mathbf v_{w_O}^{\prime}}^T \cdot \mathbf h + \log \sum_{j^{\prime}=1}^{V} \exp({\mathbf v_{w_j}^{\prime}}^T \cdot \mathbf h)\tag{21} \end{align}$$

隐藏层到输出层之间的权重更新完全和上述One-word context一样。
输入层到隐藏层之间的权重更新也与(16)式大致一样，只不过现在要更新C个上下文单词的输入词向量。每个更新公式如下：

$${\mathbf v_{W_{I,c}}}^{(new)}={\mathbf v_{W_{I,c}}}^{(old)}-\frac{1}{C} \cdot \eta \cdot \mathbf {EH}^T \tag{22}$$

注意有个$\frac{1}{C}$系数，这是式18导致的。

1.2 Skip-Gram

与CBOW模型正好相反，Skip-Gram模型是根据中心词（target word）来预测上下文单词（context words）。模型结构如下图3所示：

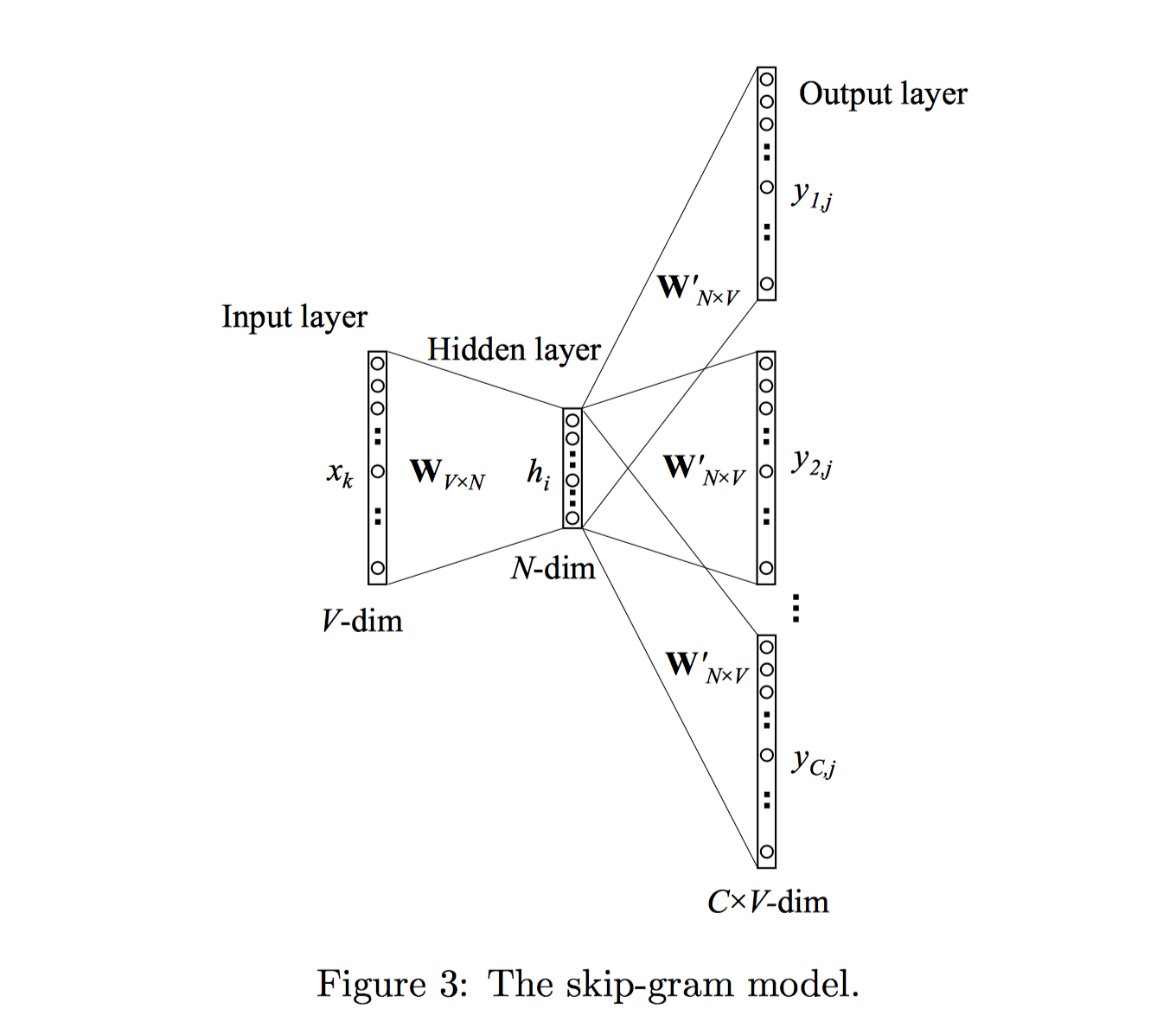
输入层到隐藏层和CBOW一样。隐藏层到输出层输出C个多项式分布，每个多项式分布代表第$c$个上下文词位置（c-th panel）上所有单词的概率分布。且$W′$由C个上下文panel共享。

$$p(w_{c,j}=w_{O,c}|w_I)=y_{c,j}=\frac{\exp(u_{c,j})}{\sum_{j^{\prime}=1}^V \exp(u_{j}^{\prime})} \tag{23}$$ $$u_{c,j}= u_j =\mathbf {v_{w_j^{\prime}}}^T \mathbf h , \ \text{for} \ c=1,2,…,C \tag{24}$$

其中，$u_{c,j}$代表输出层第c个panel的第$j$个神经元的输入值（未激活值）。
其中，$v_{w′j}$为词汇表第j个单词$w_j$的输出向量；也是取自于hidden→output权重矩阵$W^\prime$的一列。

损失函数及优化
损失函数如下，各个panel之间独立，因此将各个panel的概率连乘。且每个上下文概率计算过程中，只有一个$t_{c,j}=1$，不妨记做$j^∗_c$，其余$t_{c,j}=0$.

$$\begin{align} &E=-\log p(w_{O,1},w_{O,2},…,w_{O,C}|w_I) \tag{25}\\ &=-\log \prod_{c=1}^C \frac{\exp(u_{c,j_c^{*}})}{\sum_{j^{\prime}=1}^V \exp(u_{j^{\prime}})}\tag{26}\\ &=-\sum_{c=1}^C u_{j_c^{*} }+ C \cdot \log\sum_{j^{\prime}=1}^V exp(u_{j^{\prime}})\tag{27} \end{align}$$

1) 输出层到隐藏层
计算$E$对$u_{c,j}$的偏导，即只求每个panel中每个词未激活值的导数：

$$\frac{\partial E}{\partial u_{c,j}}=y_{c,j}-t_{c,j} :=e_{c,j} \tag{28}$$

定义V维向量，$EI={EI_1,EI_2,…,EI_V}$, 为不同上下文单词的总预测误差向量。每个分量$EI_j$代表词典中第$j$个单词，作为不同panel位置的上下文单词的预测误差和：

$$EI_j = \sum_{c=1}^C e_{c,j} \tag{29}$$

再求$E$关于权重矩阵$W^\prime$的元素$w′_{ij}$的导数，不同于CBOW，此时，一个元素$w_{ij}^\prime$和一个隐藏层神经元$h_i$、C个输出层未激活神经元$u_{c,j}$相连接。

$$\frac{\partial E}{\partial w_{ij}’}=\sum_{c=1}^C \frac{\partial E}{\partial u_{c,j}}\cdot \frac{\partial u_{c,j}}{\partial w_{ij}^{\prime}}=EI_j\cdot h_i \tag{30} \\$$

和(9)式基本一模一样，只是将$e_j$替换成$EI_j$。也就是说，某个单词$w_j$在CBOW中误差来源只有1个，因为输出中心词只有1个；而在Skip-Gram中，$w_j$可能成为C个上下文词，误差来源有C个，因为权重矩阵共享，因此C个panel中，和$h_i$以及$u_{c,j}$相连的权重$w′_{ij}$是一样的。因此，$\frac{∂_{uc,j}}{∂w′_{ij}}=h_i$是公共项，提出来，剩下的项正好是$EI_j$，即$w_j$作为上下文输出词收集的总误差。

SGD更新$w′_{ij}$:

$$\begin{align} {w_{ij}^{\prime}}^{(new)}={w_{ij}^{\prime}}^{(old)}-\eta \cdot EI_j \cdot h_i \tag{31} \end{align}$$

或者，

$$\begin{align} {\mathbf v_{w_j}^{\prime}}^{(new)}= {\mathbf v_{w_j}^{\prime}}^{(old)} - \eta \cdot EI_j \cdot \mathbf h \space \space \text{for} \ \ j=1,2,…V. \tag{32} \end{align}$$

对于每个训练样本$(w_I,w_{O,1},w_{O,2},…,w_{O,C})$，都需要使用上述公式更新词典中每个词的输出词向量。在更新每个词向量时，需要收集该词在不同上下文panel位置上的误差和，然后进行更新。一共需要$|V|$次更新。

2) 隐藏层到输入层

同样，对于input→hidden权重矩阵$W$的参数更新公式的推导过程，除了考虑要将预测误差$e_j$替换为$EI_j$外，其他也与上文公式[12]到公式[16]类似。这里直接给出更新公式：

$${\mathbf v_{w_I}}^{(new)}={\mathbf v_{w_I}}^{(old)}-\eta \cdot \mathbf{EH}^T\tag{33}$$

其中，$EH$是一个$N$维向量，组成该向量的每一个元素可以用如下公式表示：

$$EH_i=\sum_{j=1}^V EI_j\cdot w_{ij}^{\prime} \tag{34}$$

Optimization methods

2 Soft-Max vs Sigmoid

2.1 Soft-Max和Sigmoid及对应的损失函数

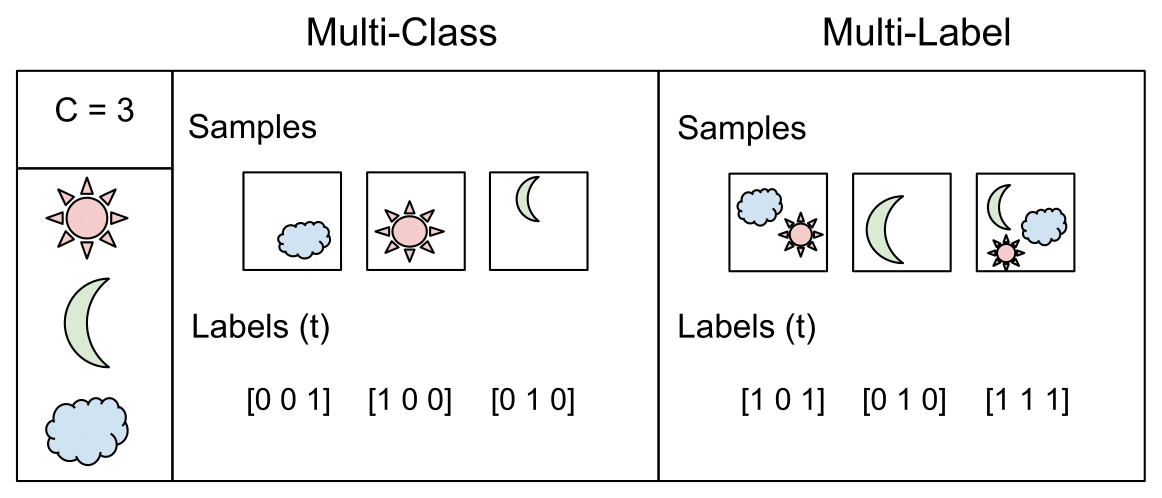
​ Multi-Class Classification： One-of-many classification. Each sample can belong to ONE of C classes. The CNN will have C output neurons that can be gathered in a vector s (Scores). The target (ground truth) vector t will be a one-hot vector with a positive class and C−1 negative classes. This task is treated as a single classification problem of samples in one of C classes.
Soft-max 函数表达式 $f(\mu_i)$

$$f\mu_i = \frac{exp(\mu_i)}{\sum_j exp(\mu_j)} \quad i,j\in \{1,2,3...\}\\ f\mu_i = \frac{exp(W_{i}^TX)}{\sum_j exp(W_j^TX)} \quad\quad i,j\in\{1,2,3..\}$$

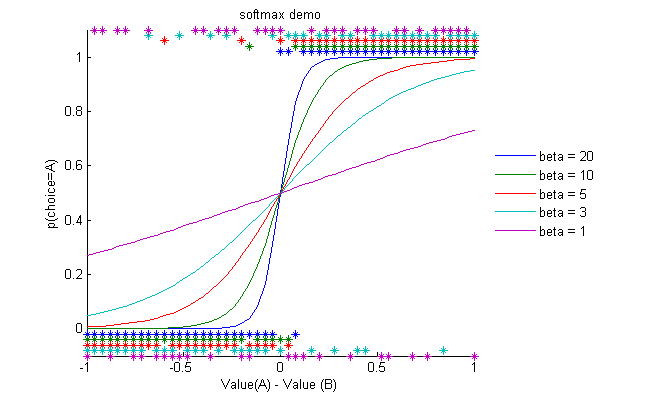
其中，$i$代表一个样本输出的后对应的one-hot结果，$j$取所有样本集合。Soft-Max仿真如图（2_1）:

Soft-Max函数仿真

其应用一般为输出层，用法如下：

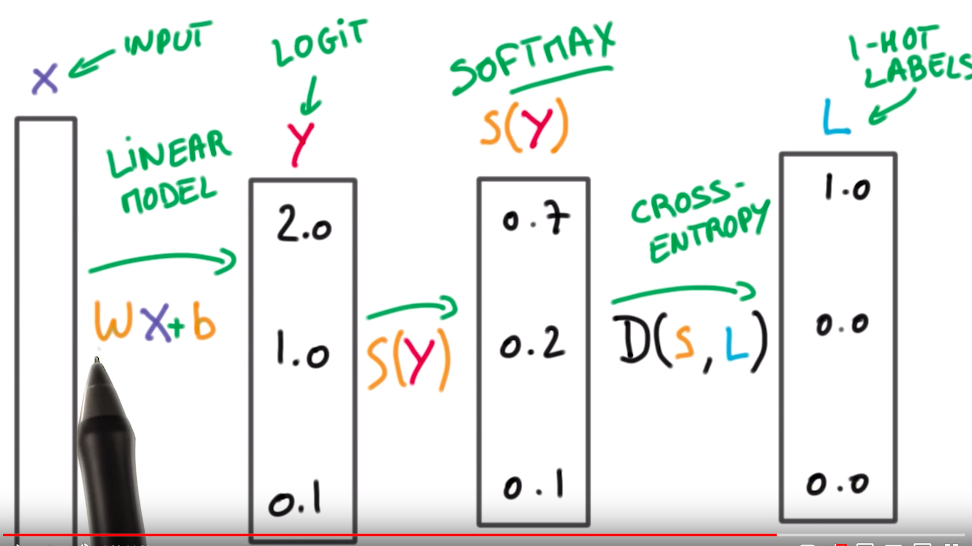
​ 上图是Soft-Max应用的全过程，包括参数层的更新，输出层的的输出，Soft-Max层的概率归一化以及真实标签与Soft-max层的损失计算。

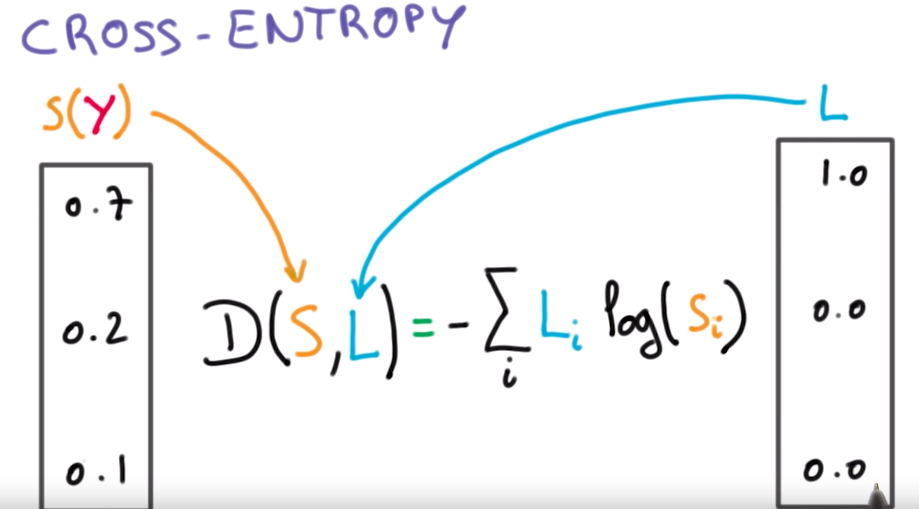
​ 必须注意的是：$S(y)$是soft-max的输出，它是一个预测值，可以命名为$\hat y$。L是真实结果值，即标签。每次输出只有一个是1，其他全为0.对于每一个输出向量，先对预测结果进行softmax，然后再利用真实值与取log之后的预测结果进行相乘（交叉熵损失函数）。如上图的例子，此时得到的结果就是$H(p,q)=-log(0.7)1-0log(0.2)-0*log(0.1)=0.5145731728297583$。所以对于这个样本损失函数是0.5145731728297583.

​ 上面的推到过程实际上就是交叉熵损失函数的计算过程，看起来很难，但是正确理解后，就会变得很容易。记住，对于一个样本的输出只能是一个One-Hot结果，也就是说只有一个值是1，其他值为0.

​ Multi-Label Classification： Each sample can belong to more than one class. The CNN will have as well C output neurons. The target vector t can have more than a positive class, so it will be a vector of 0s and 1s with C dimensionality. This task is treated as C different binary (C′=2,t′=0 or t′=1)(C′=2,t′=0 or t′=1) and independent classification problems, where each output neuron decides if a sample belongs to a class or not.
​
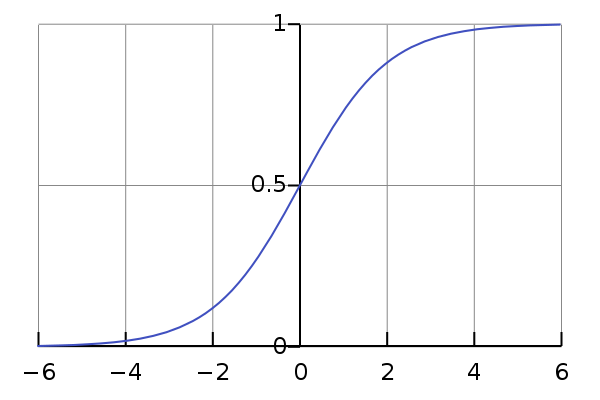
​ Two-Class Classification: 样本只会属于0,1中的一个，属于多分类$k=2$的特殊情况。sigmoid函数的意义为，将输出进行概率映射。sigmoid function$f(\mu_{i})$:

$$f\mu_j = \frac{1}{1+exp(-\mu_j)} \quad\quad\quad(2\_1)\\ \mu_j = W^TX \quad\quad\quad (2\_2)\\$$

式2为LR或者NN网络的拟合输出结果，式（2_1）为将结果进行one-hot映射。将式（2_2）代入式（2_1）即可得到式2_3：

$$f{\mu_j}=\frac{1}{exp(-W^TX)} \quad\quad\quad(2\_3)$$

sigmoid函数仿真

2.2 Soft-Max与sigmoid的同一性

1）公式证明

​ Soft-Max和Sigmoid函数的公式已经给出，当另Soft-Max函数的K=2，即一个事件只有两种可能性的时候，Soft-Max函数与Sigmoid函数一样。下面给出公式证明。
​ 对 K=2 的 Soft-Max ，有：

$$\begin{equation} p(y = 1 | x) = \frac{1}{1 + e^{-\theta^Tx}} \end{equation}$$ $$\begin{equation} p(y = 0 | x) = 1 – p(y = 1 | x) = \frac{e^{-\theta^Tx}}{1 + e^{-\theta^Tx}} \end{equation}$$

​ 而对 K=2 的 Soft-Max ，有：

$$\begin{equation} p(y = 1|x) = \frac{e^{\theta_1^Tx}}{e^{\theta_0^Tx} + e^{\theta_1^Tx}} = \frac{1}{1 + e^{(\theta_0^T – \theta_1^T)x}} = \frac{1}{1 + e^{-\beta x}} \end{equation}$$ $$\begin{equation} p(y = 0|x) = \frac{e^{\theta_0^Tx}}{e^{\theta_0^Tx} + e^{\theta_1^Tx}} = \frac{e^{(\theta_0^T-\theta_1^T)x}}{1 + e^{(\theta_0^T-\theta_1^T)x}} = \frac{e^{-\beta x}}{1 + e^{-\beta x}} \end{equation}$$

​ 从这个角度来看，sigmoid函数是Soft-Max函数k=2的情况。
2）损失Loss函数定义
二分类sigmoid
​ 而且其定义的风险函数也具有同一性，sigmoid函数风险函数可由交叉熵得到，根据上面输出的结果可知，模型输出为$p_{model}$,实际分布为$p_{data}$,从熵的角度来说，函数的拟合过程为，使得模型输出结果与实际分布尽可能的相似，从而，有交叉熵函数$H(p,q)=\sum_i^k p_{data}^i log \frac{1}{p_{model}^i}$，其中$k=2$.代入可得：

$$H(p,q) = \sum_i^{k=2} p_{data}^ilogp_{data}^i\\ H(p,q) = -(p_0logq_0+p_1logq_1)\\ H(p,q) = -(p_0logq_0+(1-q_0)log(1-q_0)) \\ Loss function = -\sum_i^N -(c_0logq_0+(1-c_0)log(1-q_0))$$

​ 因为实际分布$p_{data}=[1,0,0]^T$,$p_{model}=[0.9,0.05,0.05]^T$为模型预测分布，基于这样的基础，即可得到上式。
多分类Soft-Max
和二分类分析方法一样，基于预测的分布和实际分布相似的思想，即有：

$$H(p,q) = -\sum_i^k p_klogq_k \quad k\in\{0,1,2..\}\\$$

现以3分类case（一个样本）为例，加入实际分布为$p_{data} = [1,0,0]^T$,预测结果为：$p_{model} = [0.9,0.05,0.05]^T$,则有Loss函数为：

$$Loss = -(p_0logq_0+p_1logq_1+p_2logq_2)\\ Loss = -(c_0logq_0+c_1logq_1+c_2logq_2)\\ Loss = -(1*log0.9+0log0.05+0log0.05)\\$$

为了不失一般性，则有其Loss函数为：

$$Loss = -\sum_j^N\sum_k^K 1\cdot\{y^j=k\}logp_{model}\\ p_{model} = f(y_i^j|x^j;\theta^j) = \frac{exp(W_j^TX)}{\sum_{j^\prime}^Kexp(W_{j^\prime}^T)}$$

3 Hierarchical soft-max

​ 每个词都有个输入向量和输出向量。对每个训练样本，输入向量的优化成本不高，因为只有1个，但是输出向量的优化成本很高，需要遍历词典，优化$V$个输出向量。为了优化输出向量，对每个词，需要计算$u_j$未激活值，$y_j$(或SG中的$y_{c,j}$)激活值，误差$e_j$(或SG中的$EI_j$)，最终来更新输出向量$v_{wj′}$.

​ 显然，对于每一个训练样例都要对所有单词计算上述各值，其成本是昂贵的。特别是对于大型的词汇表，这种计算方式是不切实际的。因此为了解决这个问题，直观的方式是限制必须要更新的训练样例的输出向量的数目。一种有效的实现方式就是：hierarchical soft-max（分层soft-max），另一种实现通过负采样(negative sampling)的方式解决。

​ 实际上，这种复杂性主要原因是我们采用多分类建模的形式，共$V$个类。即认为要预测的单词是所有单词上多项式分布，那么肯定就要拟合所有单词的概率值。1种优化思路就是将多分类改成多个二分类，同时要能够很好、很快的计算训练样本实例的似然值，这种优化思路对应的方法就是hierarchical soft-max。另一种优化思路就是能不能每次训练1个样本实例的时候，不全部优化所有单词的输出向量，而是有代表性的优化某些输出向量，这种优化思路对应的方法就是negative sampling。

​ 这两种方法都是通过只优化【输出向量更新】的计算过程来实现的。在我们的公式推导过程中，我们关心的有三个值：（1）$E$，新目标函数；（2）$\frac{∂E}{∂v′_{\omega_j}}$，输出向量的更新公式；（3）$\frac{∂E}{\partial h}$，输入向量的更新公式。

Hierarchical Soft-Max

​ 使用Hierarchical Soft-max的整体神经网络结构大致是，输入层到隐藏层和上述结构类似，隐藏层神经元和二叉树所有内部节点都有连接，来传递隐向量$h$。整棵二叉树充当了输出层的角色。

​ hierarchical soft-max是一种对普通soft-max的优化(近似计算)技术，soft-max的目的是计算输入输出词的概率: $p(\omega_o|\omega_i) = \frac{exp^{(u_j)} }{\sum exp^{(u_j)}}$. hierarchical soft-max求概率的时候就需要在每个训练集上均进行计算，这样带来的计算量就非常大。计算的复杂度为$|V|$.
​ 而 hierarchical soft-max则是换了一种方式。它的思想是对单词集合不断做二分类直至每个分类中都只含有一个单词，显然这种分类的过程可以被描述成二叉树的结构。也就是说hierarchical soft-max仅仅是改变了概率的计算方式而已，在其它地方和使用传统soft-max的模型是没有区别的，当然了随机梯度下降时的公式也会不一样。计算复杂度变为$log|V|$.
​ 根据本吉奥paper（hierarchical soft-max)：Hierarchical Probabilistic Neural Network Language Model，Instead of computing directly P(Y |X) (which involves normalization across all the values that Y can take), one defines a clustering partition for the Y (into the word classes C, such that there is a deterministic function c(.) mapping Y to C), so as write as：

$$P(Y|X) = P(Y|Z,X) = P(Y|C(Y),X)P(C(Y)|X)$$

​ 映射函数可以是任何能够概率的函数，但是选取的标准要使得计算$P(C(Y)|X)$足够的简单，一般使用Sigmoid函数。
​ 原始paper的解释为（Hierarchical Soft-Max中文版）：

​ 基于上面的思想，当分类到达最后一层后（只包含一个词），其$p(Y|C(y),X) =1$,而$p(C(Y)|X)$部分可以利用Hierarchical Soft-Max的方法将复杂的soft-Max可以分解成一系列条件概率的乘积，很明显可以利用二叉树的思想去做优化（后续可以针对二叉树做优化，比如Huffman树）。

​
​ 向量$b_{i} \in\{0,1\}$ 是一个bit vector.每一层条件概率对应一个二分类问题，通过逻辑回归函数可以去拟合。对$v$个词的概率归一化问题就转化成了对$logv$个词的概率拟合问题。

​ 然后对子集$D1$和$D2$进一步划分。重复这一过程直到集合中只剩下一个word。这样就将原始大小为V的字典D转换成一棵深度为$logV$的二叉树。树的叶节点与原始字典里的word一一对应；非叶子节点对应着某一类word的集合。从根节点出发到任意的一个叶子结点都只有一条唯一的路径——这条路径也编码了这个叶子节点所属类别。
​ 对于训练样本里的一个target word $w_{t}$ ，假设其对应二叉树编码为 $\{1,0,1,….1\}$ ，则构造的似然函数为：

​

其中每一项乘积因子都是一个逻辑回归函数。可以通过最大化这个似然函数来求解二叉树的参数，即非叶子节点上的向量，用来计算游走到某一子节点的概率。Hierarchical soft-max通过构造一棵二叉树将目标概率的计算复杂度从最初的V降低到了$logV$的量级。但是却增加了词与词之间的耦合性。比如一个word出现的条件概率的变化会影响到其路径上所有非叶子节点的概率变化。间接地对其他word出现的条件概率带来影响。

损失函数优化过程
对于某个训练样本$(w_I,w_O)$，我们要优化路径$L(w_O)−1$个内部节点的输出词向量$v′_j$以及输入单词的词向量$v_{w_I}$。简化公式：

$$[\![\cdot]\!]:=[\![ n(w,j+1)=ch(n(w,j)) ]\!]\tag{42}$$ $$\mathbf v_j^{\prime}:=\mathbf v_{n_{w,j}}^{\prime}\tag{43}$$

则给定一个训练样本，损失函数为：

$$E=-\log p(w = w_O|w_I)=-\sum_{j=1}^{L(w)-1}\log\sigma([\![\cdot]\!] {\mathbf v_j^{\prime}}^T\mathbf h)\tag{44}$$

对于误差函数$E$，我们取其关于${v^\prime}_j^Th$的偏导数，得：

$$\begin{align} &\frac{\partial E}{\partial \mathbf v_j’\mathbf h}=\Big(\sigma([\![\cdot]\!]{\mathbf v_j’}^T\mathbf h)-1\Big)[\![\cdot]\!] \tag{45}\\ &= \begin{cases} \sigma({\mathbf v_j^{\prime}}^T\mathbf h)-1 ,& [\![\cdot]\!]=1 \\ \sigma({\mathbf v_j^{\prime}}^T\mathbf h), & [\![\cdot]\!]=-1 \end{cases}\tag{46}\\ &=\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j \tag{47} \end{align}$$

$t_j=1 \quad if[![⋅]!]=1, t_j=0\quad if[![⋅]!]=−1$。

接着，可以计算内部节点$n(w,j)$的输出向量表示$v^\prime_j$的偏导数：

$$\frac{\partial E}{\partial \mathbf v_j^{\prime}}=\frac{\partial E}{\partial \mathbf v_j^{\prime} \mathbf h}\cdot \frac{\partial \mathbf v_j^{\prime} \mathbf h}{\partial \mathbf v_j^{\prime}}=\Big(\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j\Big)\cdot \mathbf h\tag{48}$$ $${\mathbf v_j^{\prime}}^{(new)}={\mathbf v_j^{\prime}}^{(old)}-\eta\Big(\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j\Big)\cdot \mathbf h\space,\space \text{for} \space j=1,2,…,L(w)-1\tag{49}$$

Hierarchical Soft-max优化点关键在于式(49)，对每个训练样本，只需要更新$L(w)−1$个内部节点的输出向量，大大节省了计算时间。

为了使用反向传播该预测误差来学习训练input→hidden的权重，我们对误差函数$E$求关于隐藏层输出值的偏导数，如下：

$$\begin{align} &\frac{\partial E}{\partial \mathbf h}=\sum_{j=1}^{L(w)-1}\frac{\partial E}{\partial \mathbf v_j^{\prime} \mathbf h} \cdot \frac{\partial \mathbf v_j^{\prime} \mathbf h}{\partial \mathbf h} \tag{50}\\ &=\sum_{j=1}^{L(w)-1}\Big(\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j\Big)\cdot \mathbf v_j^{\prime} \tag{51}\\ &=\sum_{j=1}^{L(w)-1} e_j \cdot \mathbf v_j^{\prime} \tag{52}\\ &:= \mathbf{EH} \tag{53} \end{align}$$

上述$e_j$是标量，$v_{j′}$是向量。

接下来我们根据公式22就可以获得CBOW模型输入向量的更新公式，这里再写一遍。

$${\mathbf v_{W_{I,c}}}^{(new)}={\mathbf v_{W_{I,c}}}^{(old)}-\frac{1}{C} \cdot \eta \cdot \mathbf {EH}^T$$

对于Skip-Gram模型，这里的做法和前面神经网络中的SG优化过程有点不大一样，前面是把每个单词C个误差先累加起来，作为$EI$的一个分量$EI_j$（类比这里的$e_j$），然后和$v_{j′}$做点乘。而在这里，我们需要计算上下文单词中的每个单词的$EH$, 即，重复上述过程C次，每次得到一个$EH$向量，最后将C个$EH$累加，得到的向量作为该样本最终的$EH$。相当于前者先合并，后面步骤相同；后者前面步骤相同，再合并。优化的时候，将$EH$代入公式33，这里再写一遍。

$${\mathbf v_{w_I}}^{(new)}={\mathbf v_{w_I}}^{(old)}-\eta \cdot \mathbf{EH}^T$$

直观理解

Hierarchical Softmax实际上是对单词进行分组或分类。根节点为最大的类别，子节点是父节点大类别下的小类别，一直划分，直到叶子节点，到达某个具体的词。

我们可以将$σ(v\prime_j^Th)−t_j$理解为内部节点$n(w,j)$的预测误差$e_j$。即预测输出单词属于某个类别的误差。每一个内部节点的“任务”就是预测其随机游走路径是指向左孩子节点还是指向右孩子节点。每次游走到一个内部节点，询问该单词是否属于该内部节点对应的类别，是则往左走，否则往右走。

$t_j=1$意味着节点$n(w,j)$的路径指向左孩子节点，可以解释为该单词属于这个内部节点对应的类别；$t_j=0$则表示指向右孩子节点，代表该单词不属于这个内部节点对应的类别。每个训练样本决定了唯一一条路径，也就是说真实值$t_j$序列是确定的，那么优化内部节点的目标就是最小化预测类别误差。对于一个训练实例，如果内部节点的预测值非常接近于真实值，则它的向量表示$v^\prime_{j}$的更新变化很小；否则$v^\prime_j$向量指向一个适当的方向，使得该实例的预测误差逐渐减小。以上更新公式既能应用于CBOW模型，又能应用于SG模型。当在SG模型中使用该更新公式时，我们需要对C个output context words的每一个单词都重复此更新过程，也就是说C个输出上下文词，都需要从二叉树根节点游走到相应的叶子节点，各自优化自己路径上的内部节点1次。更新隐藏层到输入层时，同一个上下文单词带来的内部节点预测误差也要累加C次，并反向传播。参考公式$EIj=∑^C_{c=1}e_{c,j}$。上述二叉树构造的方法有很多，但使用Huffman树能够使得计算效率最高，保证越频繁出现的词汇，到达根节点的路径越短。

4 Negative Sampling

Negative Sampling模型的思想比Hierarchical Soft-max模型更简单。即：在每次迭代的过程中，有大量的输出向量需要更新，为了解决这一困难，Negative Sampling提出了只更新其中一部分输出向量的解决方案。
以Skip-Gram为例，最终输出的上下文单词（正样本）在采样的过程中应该保留下来并更新，同时我们需要采集一些单词作为负样本（因此称为“negative sampling”）。在采样的过程中，可以任意选择一种概率分布。将这种概率分布称为“噪声分布”（noise distribution），用$Pn(w)$来表示，可以根据经验选择一种较好的分布。在 word2vec中，作者使用了一个非常简单的采样分布，叫做unigram distribution。形式为：

$$P_n(w_j) = \frac{f(w_j)^{3/4}}{\sum_{j^{\prime}=1}^Vf(w_j^{\prime})^{3/4}} \tag{54}$$

上式，$f(w_j)$是单词$w_j$的权重，使用单词出现的频次来表示。$3/4$是分布的参数，此处是论文中使用的参数。也就是说单词出现的频次越大，越可能被选做负样本。

损失函数和优化

对于某个训练样本$(w_I,w_O)$，我们要优化真实输出单词的输出词向量$v′_{w_O}$、被选做负样本的输出单词的输出词向量$v^\prime_{w_j}$以及输入单词的词向量$v_{w_I}$。

对于某个训练样本，word2vec的论文实践证明了使用下面简单的训练目标函数能够产生可靠的、高质量的 word embeddings:

$$E=-\log \sigma({\mathbf v_{w_O}^{\prime}}^T\mathbf h)-\sum_{w_j\in W_{neg}} \log \sigma({-\mathbf v_{w_j}^{\prime}}^T\mathbf h)\tag{55}$$

其中$w_O$是该训练样本的真实输出单词（the positive sample），$v^\prime_{w_O}$是输出向量；$h$是隐藏层的输出值：在SG模型中，$h=v_{w_I}$;而在CBOW模型中，$h=\frac{1}{C}∑^C_{c=1}v_{w_{I,c}}$。$W_{neg}=\{wj|j=1,…,K\}$是基于分布$Pn(w)$采样的一系列单词。

类比Hierachical Softmax公式44，这里也都是使用sigmoid函数。第一项是真实输出单词的损失，第二项是采样的负样本作为输出单词的损失，注意sigmoid里面有个负号。上述损失非常像逻辑回归的损失(伯努利分布取对数得到的)：

$$E = - \sum_i \left(y_i log \sigma (x_i) + (1-y_i) log(1-\sigma(x_i) \right) \\ = - \sum_i \left(y_i log \sigma (x_i) + (1-y_i) log(\sigma(-x_i) \right)$$

第一项是正样本的损失，第二项是负样本的损失。在逻辑回归中，对于某个训练样本，二者取其一。在word2vec中，由于将多分类预测映射到二叉树树上，预测中心词变成预测多个二分类，二者都取。第一项根据真实训练样本，第二项根据负采样样本。优化的目标是，最大化真实样本的概率$σ(v′_{w_O}^Th)$, 最小化负样本的概率$σ((v^\prime_{w_j})^Th)$。

对于损失函数$E$，我们先求关于$(v^\prime_{w_j})^Th$的偏导数，得：

$$\begin{align} &\frac{\partial E}{\partial{ \mathbf v_{w_j}^{\prime}}^T\mathbf h}= \begin{cases} \sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h)-1 , &\text{if }\space w_j=w_O \\ \sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h), &\text {if}\space w_j\in W_{neg} \end{cases}\tag{56}\\ &\space\space\space\space\space\space\space\space\space\space\space\space\space\space =\sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h)-t_j \tag{57} \end{align}$$

其中，当$w_j$是一个正样本时，$t_j=1$；否则$t_j=0$。

接下来我们计算E关于单词$wj$的输出向量$v′_{w_j}$的偏导数：

$$\frac{\partial E}{\partial \mathbf v_{w_j}^{\prime}}=\frac{\partial E}{\partial {\mathbf v_{w_j}^{\prime}}^T\mathbf h}\cdot \frac{\partial {\mathbf v_{w_j}^{\prime}}^T\mathbf h}{\partial {\mathbf v_{w_j}^{\prime}}}=\Big(\sigma({\mathbf v_{w_j}^{\prime}}^T \mathbf h)-t_j\Big)\mathbf h \tag{58}$$

上述优化公式和Hierarchical Soft-max一样，只是$t_j$的含义不大一样。

对于某个训练样本，Negative Sampling的关键优化点在于公式（59）的更新过程只应用于词汇表的子集的输出向量，$\{wj|wj∈w_O⋃W_{neg}\}$。而并非应用于整个词汇表。通常负样本集合大小$k$取$logV$量级甚至更小。

回顾一下，Hierarchical Sampling 优化点在于，对于某个训练样本，优化输出向量时只优化路径上经过的$L(w)−1$个内部结点的输出向量。

接着利用反向传播机制，计算$E$关于隐藏层输出$h$的偏导数，$h$从1个正样本和负样本集合输出向量收集误差。

$$\begin{align} &\frac{\partial E}{\partial \mathbf h}=\sum_{w_j \in{w_O}\bigcup W_{neg}}\frac{\partial E}{\partial {\mathbf v_{w_j}^{\prime}}^T\mathbf h}\cdot \frac{\partial {\mathbf v_{w_j}^{\prime}}^T\mathbf h}{\partial \mathbf h}\tag{60}\\ &=\sum_{w_j \in{w_O}\bigcup W_{neg}}\Big(\sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h)-t_j\Big)\mathbf v_{w_j}^{\prime} \\ &= \sum_{w_j \in{w_O}\bigcup W_{neg}} e_j \cdot \mathbf v_{w_j}^{\prime}\\ &:= \mathbf{EH} \tag{61} \end{align}$$

上述公式和Hierarchical Soft-max很像，只不过Hierarchical Soft-max误差来源是$L(w)−1$个内部节点的输出向量，这里的误差来源是一个正样本以及负样本集合的输出向量。接下来的过程和Hierarchical Soft-max中一样。

将$EH$代入公式22，我们就可以得到CBOW模型关于输入向量的更新公式：

$${\mathbf v_{W_{I,c}}}^{(new)}={\mathbf v_{W_{I,c}}}^{(old)}-\frac{1}{C} \cdot \eta \cdot \mathbf {EH}^T$$

对于SG模型，我们需要计算上下文单词中的每个单词的$EH$, 即，重复上述过程C次，每次得到一个$EH$向量，最后将C个$EH$累加，得到的向量作为该样本最终的$EH$。代入公式33，这里再写一遍。

$${\mathbf v_{w_I}}^{(new)}={\mathbf v_{w_I}}^{(old)}-\eta \cdot \mathbf{EH}^T$$

参考文献：

[1] Mikolov T , Sutskever I , Chen K , et al. Distributed Representations of Words and Phrases and their Compositionality[J]. Advances in Neural Information Processing Systems, 2013, 26:3111-3119.

[2] Rong X . word2vec Parameter Learning Explained[J]. Computer Science, 2014.

[3] Hierarchical Soft-Max paper: Hierarchical Probabilistic Neural Network Language Model

[4] Hierarchical soft-max详细解释: https://zhuanlan.zhihu.com/p/74385190

[5] Soft-Max仿真: https://hannekedenouden.ruhosting.nl/RLtutorial/html/SoftMax.html

[6] CBOW和Skip-Gram经典详解: http://xtf615.com/2018/10/05/word2vec/

[7] Embedding最全解释: https://lumingdong.cn/application-practice-of-embedding-in-recommendation-system.html