PCA通俗理解和理论推导

1.The derivation of the PCA

1.1 主观理解

​ PCA算法是一种特征降维方法，该方法是一种线性降维方法。加入有两个特征，一个是房价，一个房子面积，先对结果进行降维。

Samples	X	Y
a	10	10
b	2	2
c	1	1
d	7	7
e	3	3

首先进行减均值去中心化，得到：

Samples	X	Y
a	5.4	5.4
b	-2.6	-2.6
c	-3.6	-3.6
d	-2.4	-2.4
e	-1.6	-1.6

​ 房价（$X$）和面积（$Y$）的样本协方差为（样本方差）：

$$Var(X) = \frac{1}{n-1}\Sigma_{i=1}^n (X-\mu_{X})\\ Cov(X,Y) = \frac{1}{n-1}\Sigma_{i=1}^n (X-\mu_{X})(Y-\mu_{Y})$$

​

​ PCA此时要做的工作就是对现有的特征进行线性降维，即在目前空间中找到一组基向量，然后将现有的特征映射到新的坐标空间中，同时保留特征的主要成分，删除次要成分，如：

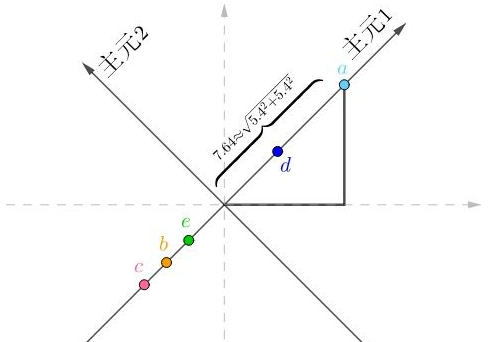
​ 很显然$a$在“主元2”上的坐标为0，把所有的房间换算到新的坐标系上：

Samples	X	Y
a	7.64	0
b	-3.68	0
c	-5.09	0
d	3.39	0
e	-2.26	0

​ 因为“主元2全都为0”，完全是多余的，只需要“主元1”就够了，这样就又把数据降维到1维，而且没有丢失任何信息。

1.2 数学推导

假设有一个两个样本，每个样本的特征空间为2，即:

$$\begin{pmatrix} index & X & Y \\ a & x_1 & y_1 \\ b & x_2 & y_2 \\ \end{pmatrix}$$

​ 其中index表示样本名称，$X,Y$二维特征。在目前的样本集下，对特征空间进行降维。假设存在一个最佳基空间，使得$a,b$在新基$e_1=(e_{11},e_{12})^T$的$e_1$上占主要成分（主元1上映射大），而在$e_2=(e_{21},e_{22})$的主元上映射很小，则应满足(应该注意的是，利用最小二乘的思路：$X_1+X_2=\Sigma_{i=1}^2X_i$)：

$$\begin{align} & X_1^2+X_2^2 = (\vec e_1\cdot \vec a)^2 + (\vec e_1\cdot \vec b)^2 \tag{1}\\ & X_1^2+X_2^2 = (x_1e_{11}+y_1e_{12})^2+(x_2e_{11}+y_2e_{12})^2 \tag{2}\\ &X_1^2+X_2^2=(x_1^2+x_2^2)e_{11}^2+2(x_1y_1+x_2y_2)e_{11}e_{12}+(y_1^2+y_2^2)e_{12}^2 \tag{3} \end{align}$$

​ 其中，$X_1,X_2$为样本在新基上的投影标量值(注：投影有正负之分)。我们的目标是使得在主元1上的投影最大，在主元2上的投影最小，这样才能省略主元2上的映射特征，以达到特征降维的目的。降维后的特征不是$X$或者$Y$,它是$X_1=\vec e_{1} \cdot \vec a$，它是一个标量，即点$\vec a$投射到单位向量$\vec e_1$上的投射长度。

​ 上式(3)中可改写为：

$$\begin{align} X_1^2+X_2^2 & = (x_1^2+x_2^2)e_{11}^2+2(x_1y_1+x_2y_2)e_{11}e_{12}+(y_1^2+y_2^2)e_{12} \nonumber\\ &=e_1^TPe_1 \tag{4} \end{align}$$

其中P：

$$P=\begin{pmatrix} x_1^2+x_2^2 & x_1y_1+x_2y_2\\ x_1y_1+x_2y_2 & y_1^2+y_2^2\\ \end{pmatrix} \tag{5}$$

​ 不难看出$P=FF^T$,对角线为特征列的方差，其他位置为特征之间的协方差，也就是说，P-Matrix是特征的协方差矩阵，并且该矩阵是对称矩阵，也可以为二次型矩阵。

由奇异值分解可知，式4可知：

$$\begin{align} X_1^2+X_2^2 &= e_1^TPe \nonumber\\ &=e_1^TU\Sigma U^Te \nonumber\\ &=n\Sigma n^T \tag{6} \end{align}$$

​ 假设$\vec n=(n_1,n_2)$，则有：

$$\begin{align} X_1^2+X_2^2 &= n\Sigma n^T \nonumber\\ & = n_1^2\sigma_1+n_2^2\sigma_2 \tag{7} \end{align}$$

​ 优化目标函数为：

$$Max: X_1^2+X_2^2 = n_1^2\sigma_1+n_2^2\sigma_2\\ subject\quad to \quad \sigma_1>\sigma_2 \quad and \quad n_1^2+n_2^2=1 \tag{8}$$

​ 由条件优化可知，满足上述条件的：$\vec n = (1,0)$:

$$\begin{align} e_1^TU=n \rightarrow e_1^T&=nU^{-1} =nU^T \tag{9} \end{align}$$

​ 求得新的基向量以后，即可求得原基中的各点在新基的映射值，即可得到线性变换后的特征结果。结果为：$X_a = \vec e\cdot\vec a $

1.3 实践结果

​ 现在有5个样本，其包含两个特征(去中心化之后)，假设这五个样本是用来预测房价的价格的样本，在预测房价价格之前，先对其进行降维。即有：

$$X=\begin{pmatrix} 5.4 \\ -2.6 \\ -3.6 \\ 2.4\\ -1.6\\ \end{pmatrix}^T \quad Y=\begin{pmatrix} 4.4 \\ -1.6 \\ -2.6 \\ 1.9\\ -2.1\\ \end{pmatrix}^T$$

​ 可知协方差矩阵为(样本协方差为：$Cov(X,Y)=\frac{1}{n}\Sigma_{i=1}^n(X-\mu_Y)(Y-\mu_Y)$)：

$$Q=\begin{pmatrix} Var(X)&Cov(X,Y)\\ Cov(X,Y)&Var(Y)\\ \end{pmatrix} =\frac{1}{5}\begin{pmatrix} \vec X\vec X^T&\vec X\vec Y^T\\ \vec X\vec Y^T&\vec Y\vec Y^T\\ \end{pmatrix} = \frac{1}{5}\begin{pmatrix} 57.2&45.2\\ 45.2&36.7\\ \end{pmatrix}$$

​ 对Q进行奇异值矩阵分解：

$$Q=\begin{pmatrix} -0.78&-0.62\\ -0.62&0.78\\ \end{pmatrix}\begin{pmatrix} 18.66&0\\ 0&0.12 \end{pmatrix}\begin{pmatrix} -0.78&-0.62\\ -0.62&0.78 \end{pmatrix}$$

​ 矩阵之前分析，主元1应该匹配最大奇异值对应的奇异向量，主元2匹配最小的奇异值对应的奇异向量。即：

$$\vec e_1=\begin{pmatrix} -0.78\\ -0.62\\ \end{pmatrix}\quad \vec e_2=\begin{pmatrix} -0.62\\ 0.78\\ \end{pmatrix}$$

​ 以此可知：

$$f_1=\begin{pmatrix} -6.94(\vec a\cdot\vec e_1) \\ 3.02(\vec b\cdot\vec e_1) \\ 4.42(\vec c\cdot\vec e_1) \\ -3.05(\vec d\cdot\vec e_1)\\ 2.55(\vec e\cdot\vec e_1)\\ \end{pmatrix} \quad f_2=\begin{pmatrix} 0.084 \\ 0.364 \\ 0.204 \\ -0.006\\ -0.646\\ \end{pmatrix}$$

​ 主元2上的特征$f_2$较小，丢掉损失的信息也非常少，这样就只保留主元1上的映射结果值，即降维特征$f_2$。

参考文献

[1] Wold S. Principal component analysis[J]. 1987, 2(1):37-52.