注:上接GBDT和XGBOOST算法推导和流程详解(PART-1)
XGBOOST算法原理及相应流程
XGBOOST相比GBDT有以下有点和改进:
1)分布式-特征切分
2)稀疏感知-缺失值直接当做特征处理
3)加权分位点进行-树构建节点分割
4)泰勒二阶导数-Newtons Methods更新方法
5)防止过拟合的方法-正则+shrinkage+subsampling
6)系统设计上更加优化
基本原理
XGBOOST-Extreme Gradient Boosting,从名字就可以看出,它利用了梯度提升的思想,但是做的更加极致,这个是因为它使用了Newton法进行更新每棵树(泰勒二阶展开)。
XGBOOST算法的流程为:
//#XGBOOST算法流程
第一步:确定损失函数,泰勒二阶展开,求解最优树权重,继而求出最优树结构和分裂标准函数。
第二步:按照分裂函数逐步一棵树一棵树去生成,值的注意的是,生成的每棵树是利用Newton法迭代的。
第三步:将每棵树进行累加,作为最终生成的数(损失最小,达到最优)。
算法结束
XGBOOST理论推导
现在给出第一步有关理论得推导:
考虑到数据最终都会分配到一棵树的叶子节点上,假设用$I_j$表示分配到叶子节点上内的样本,则下图中,共有三个叶子节点,且每个节点内的数据点共享叶子权重$w_j$。
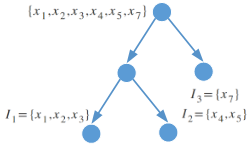
基于以上的分析23式可改写为($f_t(x)=w_q(x_i)$):
令$G_j=\sum_{x\in I_j}\partial l(y,\hat y^{(t-1)})|_{\hat y^{(t-1)}}$和$H_j =\sum_{x\in I_j}\partial^2 l(y,\hat y^{(t-1)})|_{\hat y^{(t-1)}}$,则有:
由于Loss函数是Convex and differentiable,所以:
先求出了最优叶子权重,可知最优的Loss函数为:
26式用来判断一棵树的好坏,越小,代表树的结果越好。既然这样的话,能不能想熵函数,GINI指数一样作为节点分裂函数呢?答案是肯定的,不同于GBDT节点分裂函数(MSE),XGBOOST定义了自己的分裂函数(思想和熵函数GINI一样),可以从单个节点迭代地增加分支:
总是从单个节点逐步地分割成两个分支,未分前T=1,分割后,T=2。
节点分裂策略
上面已经将第一步的理论部分进行了推导,得到了最优树权重,评判树结构好坏的Loss函数和分裂标签函数。如果不考虑计算量问题,可以通过枚举的方法建立可能树的全集,但是这在实际中显然是不现实的。三种可选的分割节点的方法:
//#3中可能的节点分割方法
1)朴素贪婪算法
2)近似贪婪算法-分位点
3)加权分位点
作者提到可以按照global的方式给出候选切分点,也可以按照local的方式给出候选切分点。
//#候选分割点的给出方法
1)global方式—在树的初始化阶段就给出候选的切分点,以后迭代(迭代新树)的过程中都使用该分割点,只计算一次(每棵树只需要计算一次),但是需要更多的候选分割点(如果想得到和Local效果相当的话),这是因为在每个分割节点上没有优化这些候选点(当前节点分裂更优地应该针对当前节点内的样本进行划分,而不是全部数据)。
2)Local方式—在每个分割节点上给出候选点。多次计算,但是只需要针对父节点给出候选分割点。
在Global方式下如果分割点足够多的话,就会得到和Local方式相似的性能。
加权分位点
不同于一般的分位点作为候选点的方法,加权分位点使用二阶导数对数据排序。之所以可以用二阶导数作为排序的标准,是因为:
加权分位点可以处理权重不同的数据,而传统的分位点方法虽然可以处理但是没有理论保证,但是加权分位点却有完整的理论证明和保证。
定义加权分位点的rank排序函数$r_{sk}$(k表示第k个特征):
通过对二阶导数进行排序同样可以达到排序的目的,那么进行为什么还要定义排序函数呢,我理解原因之一是和非加权分位点一样,在有加权($h_i$)的情况下,达到样本有权重“均衡”地分配的目的。
稀疏感知
XGBOOST对于缺失值可以不做处理,直接进行训练,也可以理解成XGBOOST算法将缺失值作为数据点,输入到模型训练中,然后找到缺失值最好的分裂点。但是这样做有疑问的地方:
1)缺失值都已经缺失了,如何判断缺失值分裂到左边获得的得分增益高,还是右边获得得分增益高?
2)”Github上XGBOOST作者说,分到左边或者右边,依据是训练时损失函数的降低程度“,但是如果值都missing了,到底怎么计算呢?
论文给出的稀疏感知的算法过程没有详细的计算过程:
//#稀疏感知分裂算法流程
将数据按照未缺失值进行递增排序
利用分割函数对未缺失值进行分割并统一将缺失样本分到右边
找到最佳分割点
将数据按照未缺失值进行递减排序
利用分割函数分割未缺失值-将缺失样本统一分到左边
找到最佳分割点
输出最大gain的缺失值分配方向
那么就遇到上面的问题,我不知道缺失值是多少,我怎么计算放哪边更好,或者说怎么算放哪边损失降级的更大。根据[4]所述,结合我的理解,它应该是这样处理的:
//#我理解的XGBOOST处理缺失值的方法
回归问题:假设损失函数是MSE
1)按照未缺失值遍历,按照分裂函数给出分裂结果,同时将缺失值放到右边(缺失值虽然特征缺失,但是label肯定是有的),将缺失值的label与未缺失值计算结果进行计算(MSE(w_i,label)),记录此时分裂方法的Gain,一次遍历,选择Gain最大的分割点和缺失值分配方法
2)重复上面的做法,此时将缺失值统一放到左边,记录Gain,同样选取最大Gain作为切分方法和缺失值分配方法。
3)找到1)2)中最大的Gain,将相应的切分方法和缺失值分配方法作为处理方法
分类问题:
分类问题处理方法和回归思想一样,计算损失使用的函数为交叉熵($-y_ilog\frac{1}{1+e^{F_m(x)}}$),$F_m(x)$为未缺失样本给出的分裂叶子节点权重,$y_i$为缺失值样本的标签。
将未缺失样本的损失加上缺失样本的损失,选择最小的,进而就可以判断分裂节点的同时,又能决策缺失样本的分裂问题。
上面是我的理解。但是有一点疑惑,既然可以计算所有缺失样本统一分到左边或者右边的损失,为什么不对缺失样本进行一一判断呢,这样可以使得损失更小(相比统一放到左边或者右边)?也许是XGBOOST作者考虑到计算量的问题。
系统设计上的优点
分块并行
在建树的过程中,最耗时是找最优的切分点,而这个过程中,最耗时的部分是将数据排序。为了减少排序的时间,提出Block结构存储数据。Block结构数据按列存储,可以同时访问所有的列,很容易实现并行的寻找分裂点算法。此外也可以方便实现之后要讲的out-of score计算。
缓存优化 – Cache-aware Access
缓存预取,对每个线程分配一个连续的buffer,读取梯度信息并存入Buffer中
Blocks for Out-of-core Computation(外存计算)
当数据量太大不能全部放入主内存的时候,为了使得out-of-core计算称为可能,将数据划分为多个Block并存放在磁盘上。
- 计算的时候,使用独立的线程预先将Block放入主内存,因此可以在计算的同时读取磁盘
- Block压缩,貌似采用的是近些年性能出色的LZ4 压缩算法,按列进行压缩,读取的时候用另外的线程解压。对于行索引,只保存第一个索引值,然后用16位的整数保存与该block第一个索引的差值。
- Block Sharding, 将数据划分到不同硬盘上,提高磁盘吞吐率
实际操作碰到的问题
问题1:用户均分布于高分段,且训练集正负样本1:1,跨期测试其大多分布于高分段。图1和图2正负样本权重(scale_pos_weight=3)分别为3时的样本有偏现象。
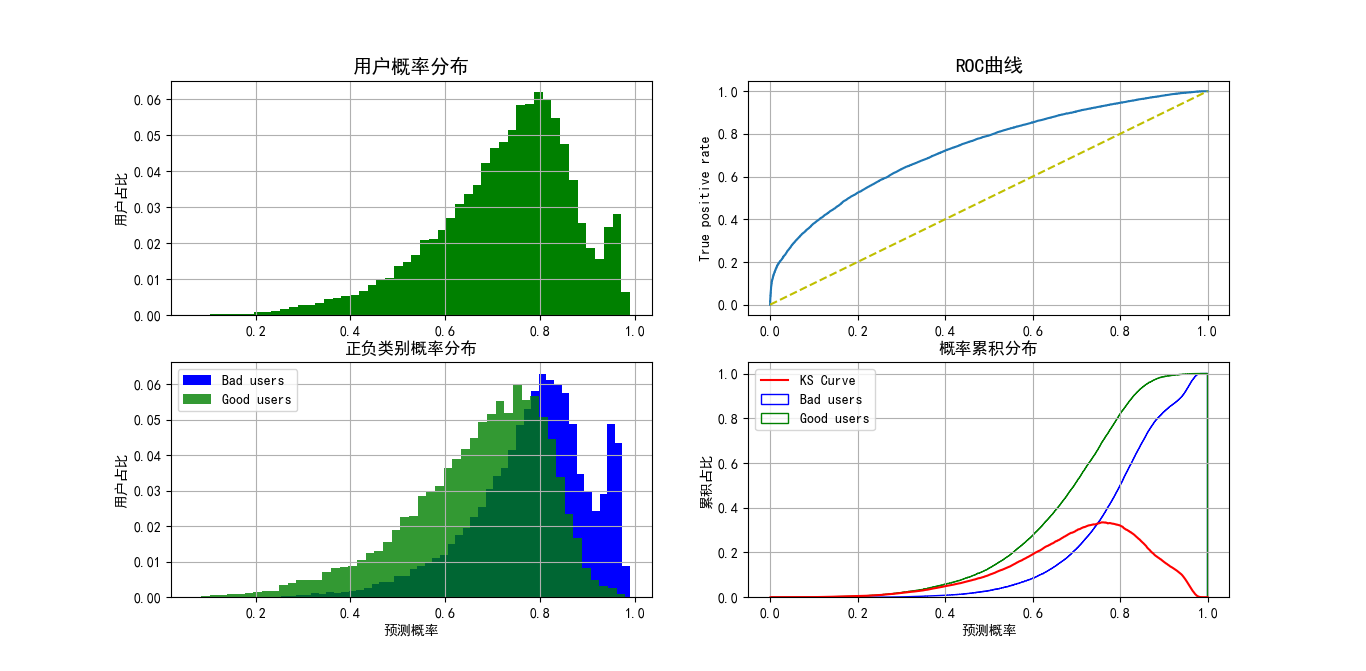
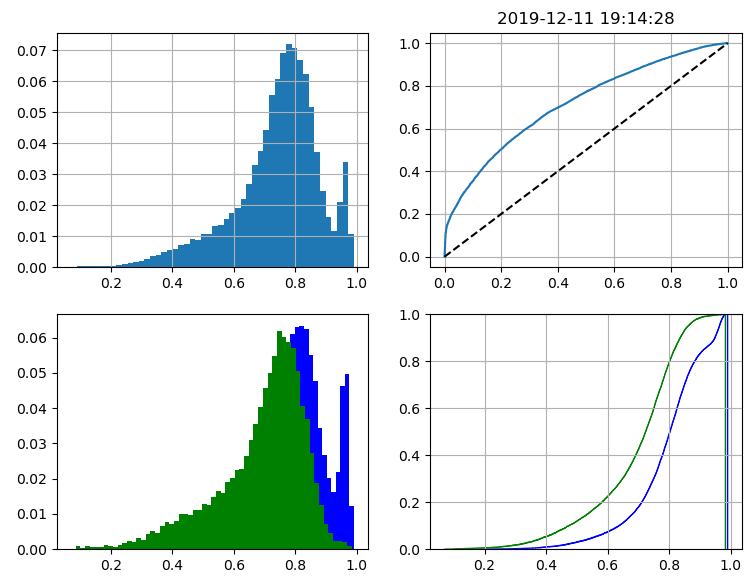
因为实际上我的样本是1:1,训练的时候增加了正样本的权重,所以训练的结果右偏。
改变正负样本权重为1:1(scale_pos_weight=1)后,训练结果如下图所示:
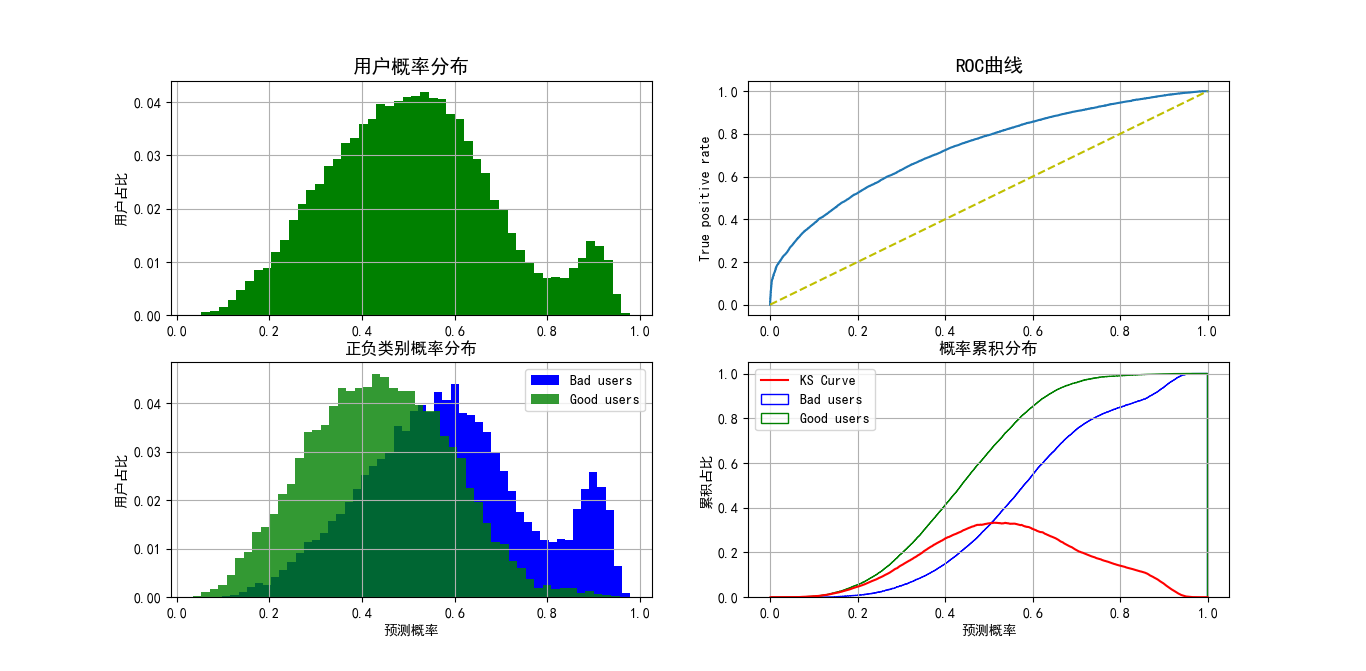
参考文献:
[1] GDBT做分类的方法: https://www.cnblogs.com/modifyrong/p/7744987.html
[2] GBDT 梯度计算方法: https://zhuanlan.zhihu.com/p/46445201
[3] SoftMax梯度推导: http://onlynice.me/2017/11/18/Softmax回归及其softmax-cross-entropy-loss推导/